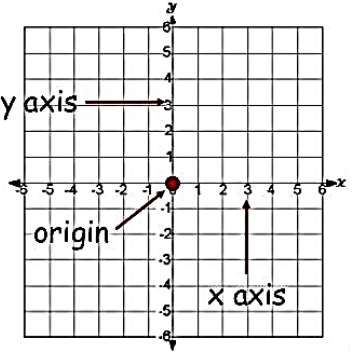
Class 9 Maths introduces you to a new world of concepts, theorems, applications, and techniques to solve mathematical problems Class 9 Maths Chapter 3 in this syllabus focuses on the concepts of coordinate geometry Here you will learn what coordinate axes are and how a point is plotted using the concepts of Cartesian CoordinatesThere are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –Thoroughly understand the concept of the Cartesian plane with TopperLearning's NCERT Solutions for CBSE Class 9 Mathematics Chapter 3 Coordinate Geometry Learn to plot points in a Cartesian plane with our Maths textbook solutions Our experts include crucial concept insights in these model answers to give you more information for conceptual clarity

Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
(x-y)^3 formula class 9
(x-y)^3 formula class 9- Coordinate Geometry Class 9 Extra Questions Very Short Answer Type Question 1 Write the signs convention of the coordinates of a point in the second quadrant Question 2 Write the value of ordinate of all the points lie on xaxis Question 3 Write the value of abscissa of all the points lie on yaxisSelina Concise Mathematics Part I Solutions for Class 9 Mathematics ICSE, 27 Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) All the solutions of Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) Mathematics explained in detail by experts to help students prepare for their ICSE exams




Draw The Graphs Of The Equations X 3 X 5 And 2x Y 4 0 Also Find The Area Of The Quadrilateral Youtube
Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) Ex 25, 9 Verify (ii) x3 y3 = (x y) (x2 xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y 9 (a – b) 3 = a 3 – b 3 – 3ab(a – b) 10 (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2xz 11 (x y – z) 2 = x 2 y 2 z 2 2xy – 2yz – 2xz 12 (x – y z) 2 = x 2 y 2 z 2 – 2xy – 2yz 2xz 13 (x – y – z) 2 = x 2 y 2 z 2 – 2xy 2yz – 2xz 14 x 3 y 3 z 3 – 3xyz = (x y z)(x 2 y 2 z 2 – xy – yz − xz) 15 x 2 y 2 = 12(x y) 2 (x – y) 2 16NCERT Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 43 Plot the ordered pairs (0, 4), (1,3) and (2,2) on the graph paper Joining these points, we get a straight line AB as shown Plot the ordered pairs (0, 2), (1, 1) and (2, 0) on the graph paper
Free system of equations calculator solve system of equations stepbystep23x 2 – 5x 1;Important Questions for Exam Class 9 Chapter 1 Class 9 Number Systems Chapter 2 Class 9 Polynomials Chapter 3 Class 9 Coordinate Geometry Chapter 4 Class 9 Linear Equations in Two Variables Chapter 5 Class 9 Introduction to Euclid's Geometry Chapter 6 Class 9 Lines and Angles Chapter 7 Class 9 Triangles
= (x 2 y 2 2xy ) (x y) As (x y) 2 = x 2 2xy y 2 =(x y) 2 (x y) =(x y)(x y 1) Heron's Formula Class 9 Extra Questions Short Answer Type 2 Question 1 Find the area of a triangle whose sides are 11 m, 60 m and 61 m Solutioin Let a = 11 m, b = 60 m and c = 61 m Question 2 Suman has a piece of land, which is in the shape of a rhombus She wants her two sons to work on the land and produce different cropsAll questions and answers from the Rs Aggarwal 19 Book of Class 9 Math Chapter 3 are provided here for you for free You will also love the adfree experience on Meritnation's Rs Aggarwal 19 Solutions All Rs Aggarwal 19 Solutions for class Class 9 Math are prepared by experts and are 100% accurate




Mathematics Class 9th Chapter 4 Solution




Solve 2xy X Y 3 2 Xy 2x Y 3 10 Mathematics Topperlearning Com X2oivz99
Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2Solution In 3x 1, the coefficient of x is 3(x 3) (x – 3) = x 2 – 3 2 = x 2 – 9 Problem Solve (x 5) 3 using algebraic identities Solution We know, (x y) 3 = x 3 y 3 3xy(xy) Therefore, (x 5) 3 = x 3 5 3 3x5(x5) = x 3 125 15x(x5) = x 3 125 15x 2 75 = x 3 15x 2 0 (Answer)




R D Sharma Solutions Class 9th Ch 13 Linear Equations In Two Variables Exercise 13 3




If 3 X Y 81 And 81 X Y 3 Then The Value Of X Y Is
Class 9 Maths Formulas By Chapters Chapter 2 – Polynomials Chapter 3 – Coordinate Geometry Chapter 7 – Triangles Chapter 8 – Quadrilaterals Chapter 9 – Areas of Parallelograms and Triangles Chapter 10 – Circles Chapter 12 – Heron's Formula Chapter 13 – Root Maths Formulas Square Root If x 2 = y then we say that square root of y is x and we write √y = x So, √4 = 2, √9 = 3, √36 = 6 Cube Root The cube root of a given number x is the number whose cube is x• x 3 – y 3 = (x – y) (x 2 xy y 2) DEGREE OF A POLYNOMIAL • The exponent of the term with the highest power in a polynomial is known as its degree f(x) = 8x 3 – 2x 2 8x – 21 and g(x) = 9x 2 – 3x 12 are polynomials of degree 3 and 2 respectively




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube



Revision Notes For Maths Chapter 3 Coordinate Geometry Class 9th Askiitians
NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry in Hindi Medium and English Medium free to download in PDF form updated for new academic session 2122 based on latest CBSE Curriculum UP Board students can get the UP Board Solutions for Class 9 Maths Chapter 3 from here MCQs from Class 9 Maths Chapter 3 – Coordinate Geometry are provided here to help students prepare for their upcoming Maths exam 1 If the coordinates of a point are (0, 4), then it lies in Explanation Since, x=0 and y=4 Hence, the point will lie in negative yaxis 4 units far from the origin 2 Class 9 NCERT Solutions Chapter 3 Coordinate Geometry Exercise 33;




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
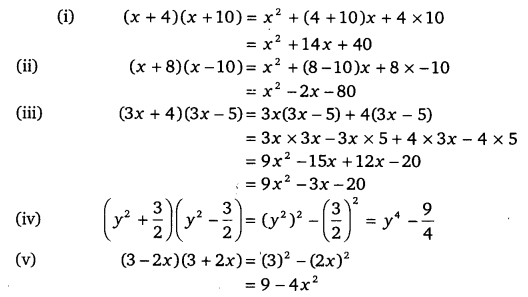



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
Sum of these numbers is 11 Cubing on both sides gives (x y) 3 = 5 3 x 3 y 3 3xy(x y) = 125 x 3 y 3 72(5) = 125 x 3 y 3 = 125 360 = 485 So, difference of their cubes is 485 Cubing both sides, we get (x y) 3 = 11 3 x 3 y 3 3xy(x y) = 1331 Misc 9 Evaluate x y xy y xy x xy x y Chapter 4 NCERT Chapter 4 Class 12 Determinants Serial order wise MiscellaneousAns Class 9 is a very important phase of a student's life Many students start aiming and preparing for higher studies from this stage Hence preparing all the chapters skillfully are quite important Maths is regarded as a very important subject at this stage Formulas are also very important to learn in order to ace in Class 9 Mathematics




The Graph Of The Linear Equation 2x 3y 6 Cuts The Y Axis At The Point Youtube




Solve Each Other Pair Of Equation Given Below Using Elimination Method 3 X 2 Y 9 Xy 9 X 4 Y 21 Xy Mathematics Topperlearning Com 59bn37qq
Maths identities class 9 usually are used to make complex calculations simpler without using the automated electronic calculators There are many Maths identities class 9 students can use to lessen their efforts in complex Mathematical problems 9th class algebra has a huge list of algebraic identities for class 9 students to make use ofAlgebra Solve by Substitution xy=3 , xy=9 x y = 3 x y = 3 , x − y = 9 x y = 9 Subtract y y from both sides of the equation x = 3− y x = 3 y x−y = 9 x y = 9 Replace all occurrences of x x with 3−y 3 y in each equation Practice as much as you can to understand the Maths Class 9 Formulas 3 Is there a Website that provides all Maths formulas for Class 9?




If X Y 3 X Y 2 Then What Is The Value Of X 3 Y 3




Algebra Formulas For Class 9 Pdf Download Free Here
Sin(xy) = sin(x)cos(y)cos(x)sin(y) cos(xy) = cos(x)cos(y)–sin(x)sin(y) tan(xy) = (tan x tan y)/ (1−tan x •tan y) sin(x–y) = sin(x)cos(y)–cos(x)sin(y) cos(x–y) = cos(x)cos(y) sin(x)sin(y) tan(x−y) = (tan x–tan y)/ (1tan x • tan y) Double Angle IdentitiesDefinition An equation of the type axbyc = 0, where a,b,c are real numbers such that a and b are nonzero, is called a linear equation in two variables x and y Example xy5 = 0 is a linear equation in the two variables (unknowns) x and y Note that x=2 and y=3 satisfy this linear equationFree PDF download of Chapter 5 Introduction to Euclids Geometry Formula for Class 9 Maths To Register Online Maths Tuitions on Vedantucom to clear your doubts from our expert teachers and solve the problems easily to score more marks in your CBSE Class 9 Maths Exam



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




X Y 3 Formula Class 9 Novocom Top
Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5) Solution Question 9 The xcoordinate of a point P is twice its ycoordinate If P is equidistant from the points Q (2, 5) and U (3, Math formula for class 9 In this article, we have provided all the essential formulas It is designed for your convenience so that you can reach it directly and sort out any of your problems easily Math formula for class 9 includes all the necessary chapters which you need most for your board exams and also daily revision You don't have (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx (x y) 3 = x 3 y 3 3xy(x y) (x – y) 3 = x 3 – y 3 – 3xy(x – y) x 3 y 3 z 3 – 3xyz = (x y z) (x 2 y 2 z 2 – xy – yz – zx) Polynomials Class 9 Examples Example 1 Write the coefficients of x in each of the following 3x 1;




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Draw The Graphs Of The Equations X 3 X 5 And 2x Y 4 0 Also Find The Area Of The Quadrilateral Youtube
X 3 – y 3 = (x – y) (x 2 xy y 2) x 2 y 2 z 2 – xy – yz – zx = \(\frac{1}{2}\) (x – y) 2 (y – z) 2 (z – x) 2 Class 9 Maths Formulas For TrianglesVerify Formula Need to verify formula is right or wrong put the value of a =2 and b=3 put the value of a and b in the LHS put the value of a and b in the RHS Therefore LHR = left hand side, RHS = right hand side Verify FormulaStudents can make use of our website to access all the Class 9 Maths Formulas as per the topics to



Standard Identities Of Binomials And Trinomials Equations Examples




X 3 Y 3 X 3 Y 3 Formula Proof Youtube
Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as; Check the below NCERT MCQ Questions for Class 9 Maths Chapter 3 Coordinate Geometry with Answers Pdf free download MCQ Questions for Class 9 Maths with Answers were prepared based on the latest exam pattern We have provided Coordinate Geometry Class 10 Maths MCQs Questions with Answers to help students understand the concept very wellNCERT Solutions for Class 9 Maths Chapter 4 Linear Equations In Two Variables Exercise 43 1 Draw the graph of each of the following linear equations in two variables (i) xy = 4 Solution To draw a graph of linear equations in two variables, let us find out the points to plot




Mathematics Class 9th Chapter 4 Solution




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
Question 9 Verify (i) x 3 y 3 = (x y)(x 2 – xy y 2) (ii) x 3 – y 3 = (x – y) (x 2 xy y 2) Solution (i) ∵ (x y) 3 = x 3 y 3 3xy(x y) ⇒ (x y) 3 – 3(x y)(xy) = x 3 y 3 ⇒ (x y)(x y)23xy = x 3 y 3 ⇒ (x y)(x 2 y 2 – xy) = x 3 y 3 Hence, verified (ii) ∵ (x – y) 3 = x 3 – y 3 – 3xy(x – y) ⇒ (x – y) 3 3xy(x – y) = x 3 – y 3Given x y = 5 and xy = 24 (x>y) (x y) 2 = (x y) 2 4xy = 25 96 = 121 So, x y = 11; Algebra Formulas Important Algebraic Identities Algebraic identities comprise various equality equations consisting of different variables a) Linear Equations in One Variable A linear equation in one variable has the maximum of one variable present in order 1It is depicted in the form of ax b = 0, where x is represented as the variable



Algebra Formula Solved Examples List Of Algebraic Formulas



1
Ex 121 Class 9 Maths Question 6 An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm Find the area of the triangle Solution Let the sides of an isosceles triangle be a = 12cm, b = 12cm,c = x cm Since, perimeter of the triangle = 30 cm ∴ 12cm 12cm x cm = 30 cm ⇒ x = (30 – 24) = 6Math Formula for Class IX For most of the students, class 9 th Maths is the nightmare and the formulas are very difficult to learn If you will not show a positive attitude towards learning mathematics then there are chances that may lose your interest from learning {3} y^{3} = \\(x y) (x^{2} – xy y^{2})\)We hope the NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Ex 31, help you If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry Ex 31, drop a comment below and we will get back to you at the earliest



If X Y 3 X Y 1 Then What Is X Y Quora



Q Tbn And9gctrh1ypujwtooh8c3vpasyfikri1qchje80vre Ccrxfnsx8i 7 Usqp Cau
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Class IX, the preboard class keeps the foundation of class XI, syllabus being similar Hence one should start its preparation at the earliest Oureducationin will be helping you in doing so Keeping notes is easy when every formula is available on a single page Here are some formulae from two very important chapters, Thermodynamics andClass 9 NCERT Solutions Chapter 4 Linear Equations in two variables Exercise 41 (n value) in the data set is odd then the formula to calculate median is Median = ((n 1)/2) th term If the number of values (n value) in the data set is even then the formula to
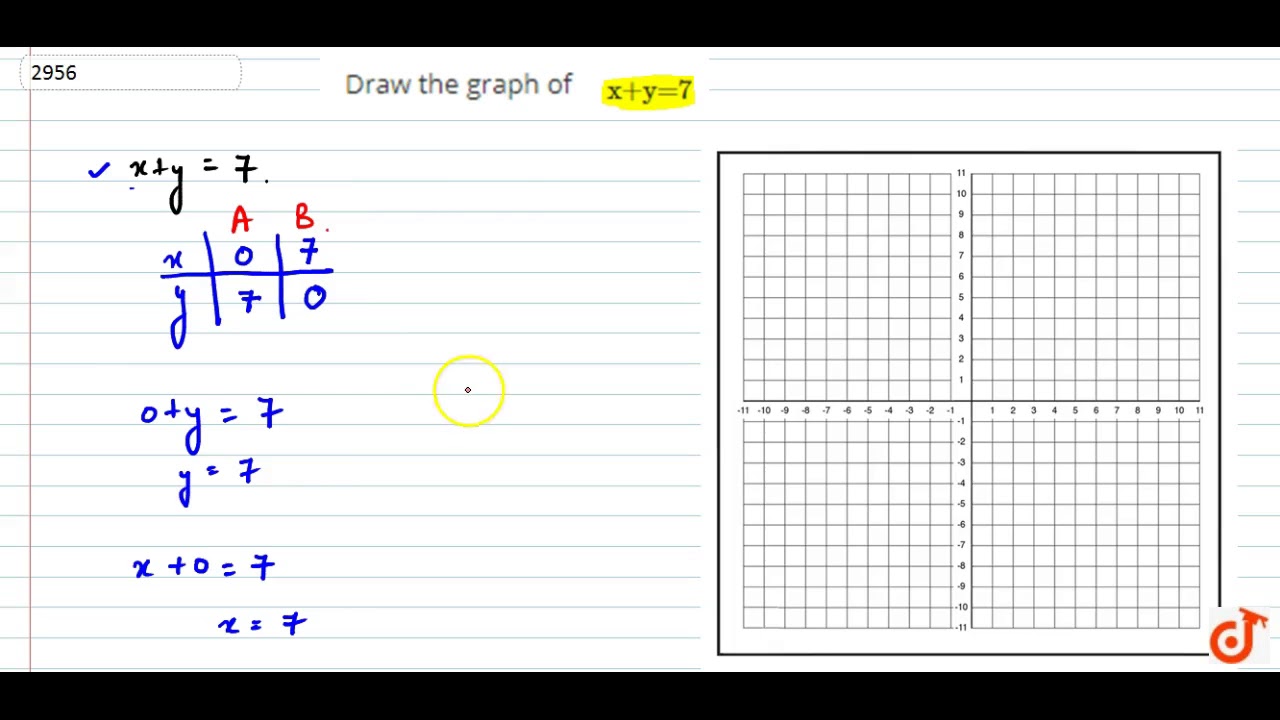



Draw The Graph Of X Y 7 Youtube




Maths Formulas For Class 9 Cbse Important Maths Formulas
X y = 5 The graph of the given line is shown below From the given line x y = 5, we get Again we know that equation of any straight line in the form y = mx c, where m is the gradient and c is the intercept Again we have if slope of a line is tan θ then inclination of the line is θ Now from the equation (A) , we have And c = 5




Section Formula Definition Vector Formula Cases Videos And Examples




Mathematics Class 9th Chapter 4 Solution
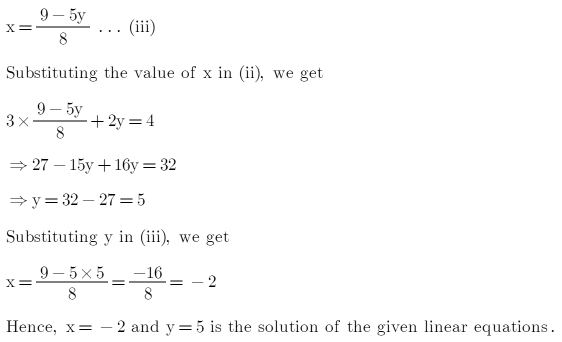



By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll




Ml Aggarwal Icse Solutions For Class 9 Maths Chapter 4 Factorisation A Plus Topper




Ex 10 3 1 Reduce Equations Into Slope Intercept Form Ex 10 3




For What Value Of N Is Following A Homogeneous Differential Equation




R D Sharma Solutions Class 9th Ch 13 Linear Equations In Two Variables Exercise 13 3




What Is The Formula Of Math A B 3 Math Quora




Http Www Aplustopper Com Solving A Quadratic Equation By Factoring Quadratics Maths Solutions Quadratic Equation




Constant Of Proportionality From Equation Video Khan Academy




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables



Coordinate Geometry Class 9 Notes With Solved Examples




Example 6 Draw The Graph Of X Y 7 Chapter 4 Examples




Ex 3 1 6 Find X Y Z From Equation Chapter 3 Matrices




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials



Class 9 Maths Important Questions For Linear Equations In Two Variables
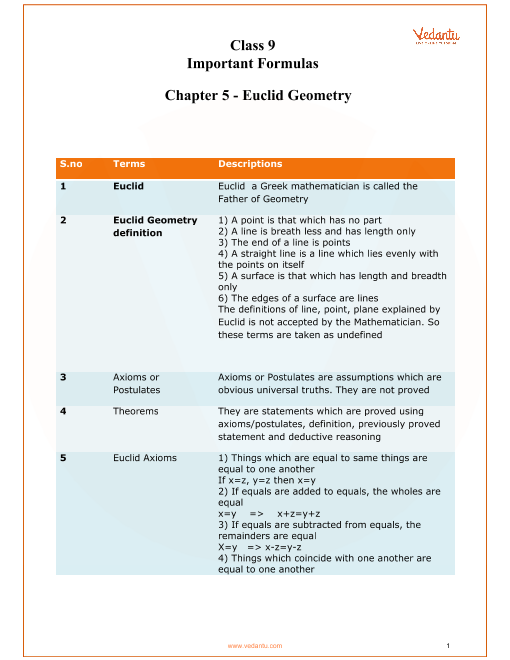



Cbse Class 9 Maths Chapter 5 Introduction To Euclids Geometry Formulas




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Pdf
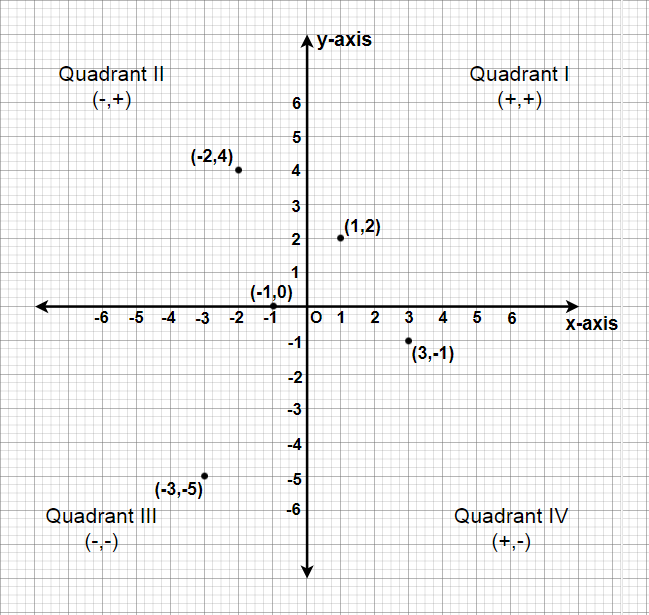



Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks




How To Graph X Y 3 Youtube




Distance Of Point From A Line Meaning Formulas Videos And Examples




Composite Functions And Invertible Function Concepts Videos Examples



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3
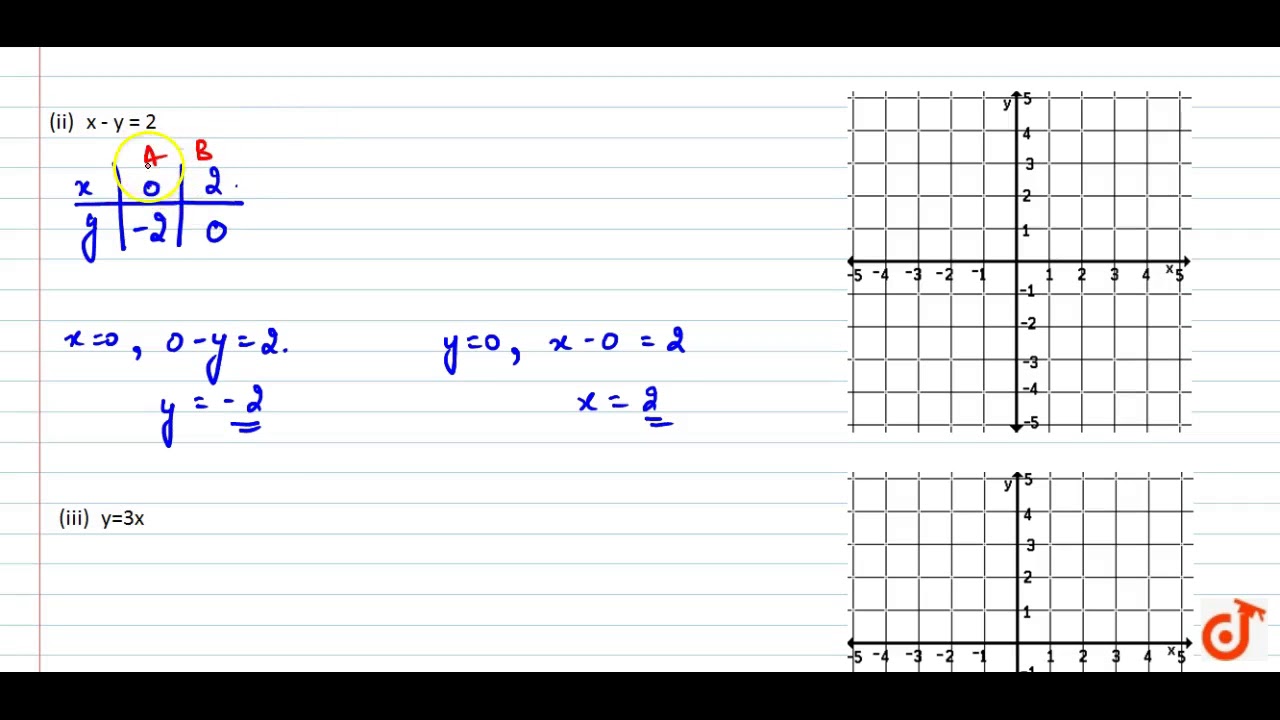



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y Youtube




Which Of The Following Expressions Are Polynomials In Case Of A




Maths Formulas For Class 9 Ncert All Chapters Math Formulas




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




Ncert Solutions For Class 9 Maths Chapter 6 Lines And Angles




Section Formula Internal And External Division Coordinate Geometry Geeksforgeeks



Polynomials Class 9th Formula Studyrankersonline




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




By Substitution Method Find X 2 2y 3 1 And X Y 3 3 Brainly In




Ex 3 5 1 Which Pair Has Unique No Solution Or Infinitely




Cbse Class 9 Maths Chapter 3 Coordinate Geometry Formulas




X Y 3 Formula Class 9 Novocom Top




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Selina Solutions Class 9 Concise Maths Chapter 5 Factorisation Download Free Pdf




Important Maths Formulas For Class 6 7 8 9 10 11 12 Cbse Board Version Weekly




If X Y 9 X Y 14 Then Find X Y Youtube




Important Maths Formulas For Class 6 7 8 9 10 11 12 Cbse Board Version Weekly




Algebraic Identities Of Polynomials A Plus Topper
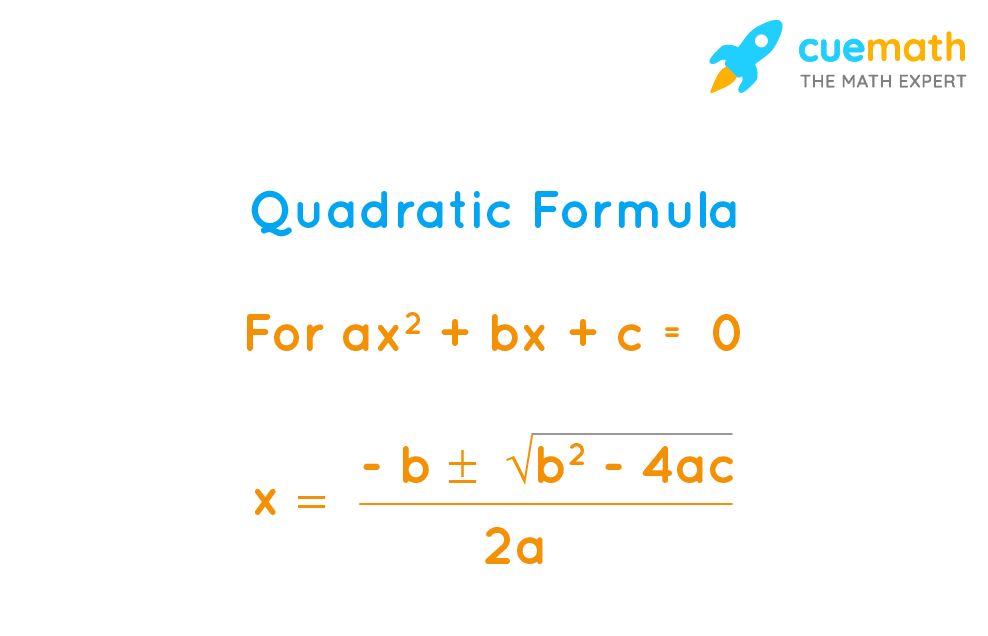



Algebra Formula Solved Examples List Of Algebraic Formulas




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




If X 1 2 3 4 5 Y 1 3 5 7 9 Then Find The Value Of n




Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15




Rs Aggarwal Class 9 Solutions Chapter 3 Factorisation Of Polynomials



Q Tbn And9gcssybq V6w5c4ycihm 68bcxq8mejb95tggv4bgo Rjkxe7bjcq Usqp Cau




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




Rd Sharma Class 9 Chapter 5 Factorization Of Algebraic Expressions Free Pdf




Factorise X 5 Y 5




Maths Formulas For Class 9 Learn Cram




Class 9 Maths Ws 4 Worksheet



Rd Sharma Class 9 Chapter 4 Algebraic Identities Free Pdf




Graphing A Linear Equation Y 2x 7 Video Khan Academy




Algebra Formulas List Of Important Algebraic Expressions Formulas




Exercise 2e Of Rs Aggarwal Class 9 Maths Solutions Chapter 2 Polynomials




Coordinate Geometry Chapter 3 Cbse Class 9 Ix Maths Youtube
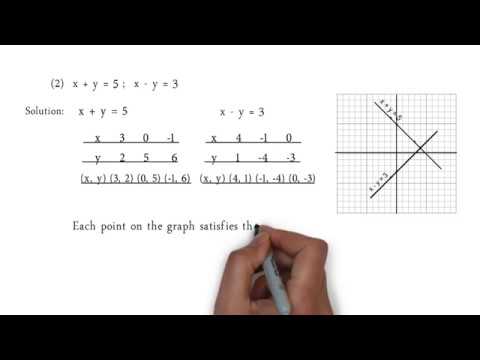



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube



If X Y 3 X Y 1 Then What Is X Y Quora



What Is The Answer Of X Y Quora



1




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities
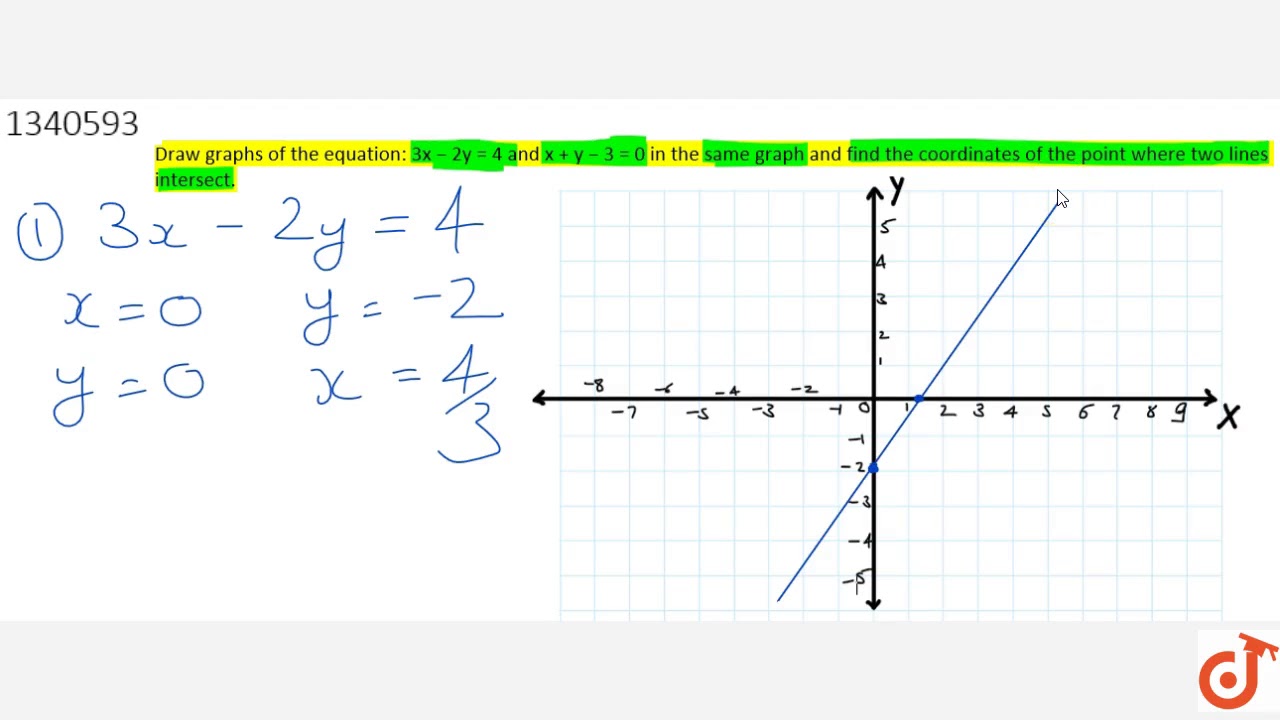



Draw Graphs Of The Equation 3x 2y 4 And X Y 3 0 In The Same Graph And Find The Coordinat Youtube
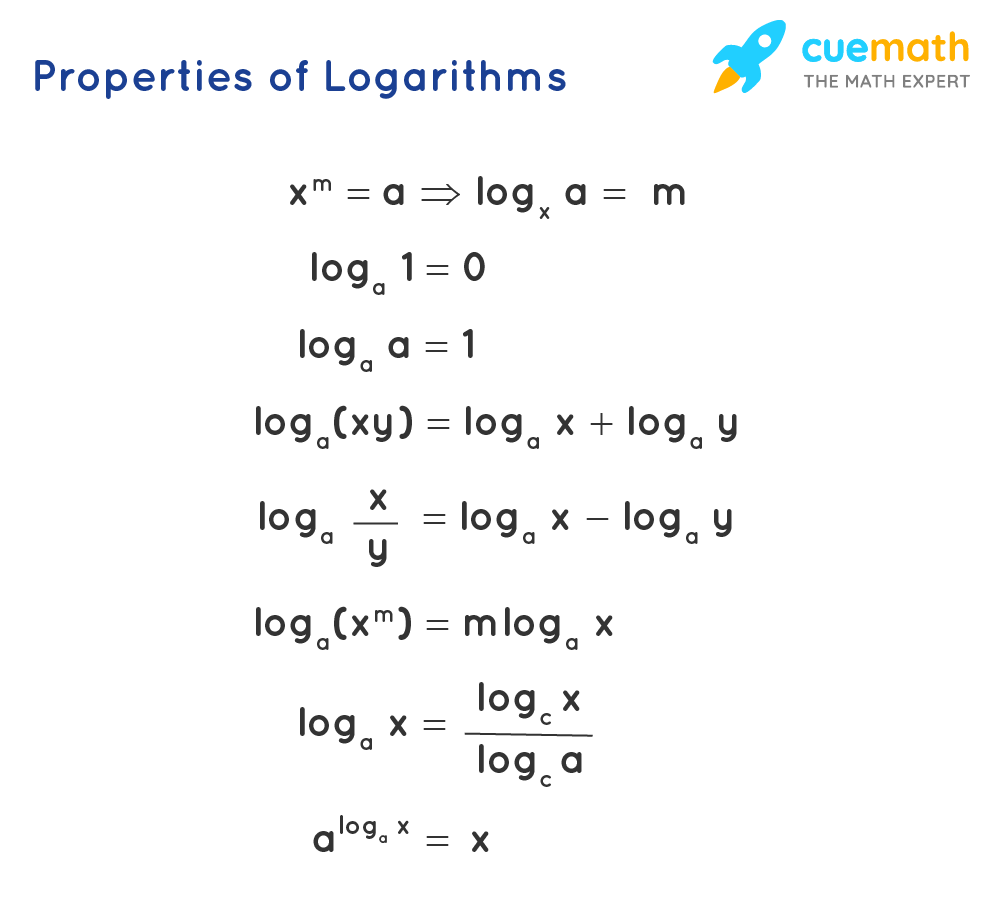



Algebra Formula Solved Examples List Of Algebraic Formulas




Polynomial Formula Meaning Types Polynomial Identities
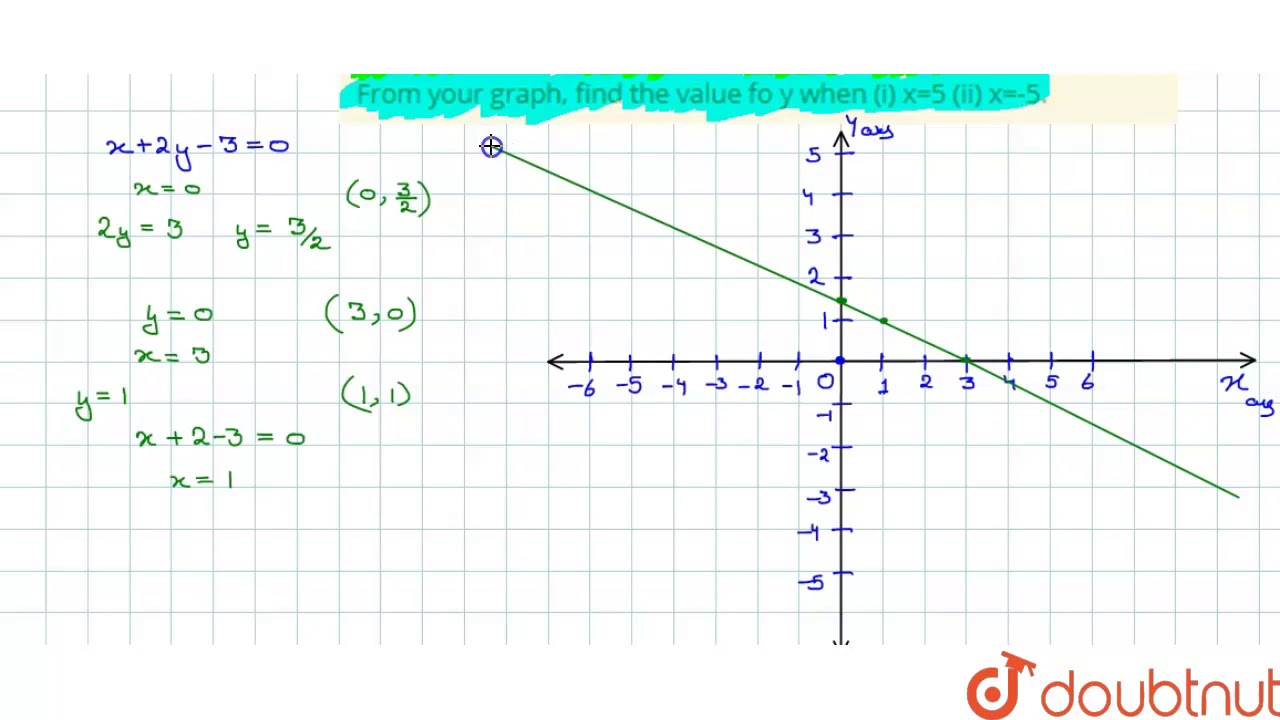



Draw The Graph Of The Equation X 2y 3 0 From Your Graph Find The Value Fo Y When I X 5 I Youtube




Standard Identities Of Binomials And Trinomials Equations Examples




Mathematics Class 9th Chapter 4 Solution




If X Y 2 Z 2 4 Y Z 2 X 2 9 Z X 2 Y 2 36 What
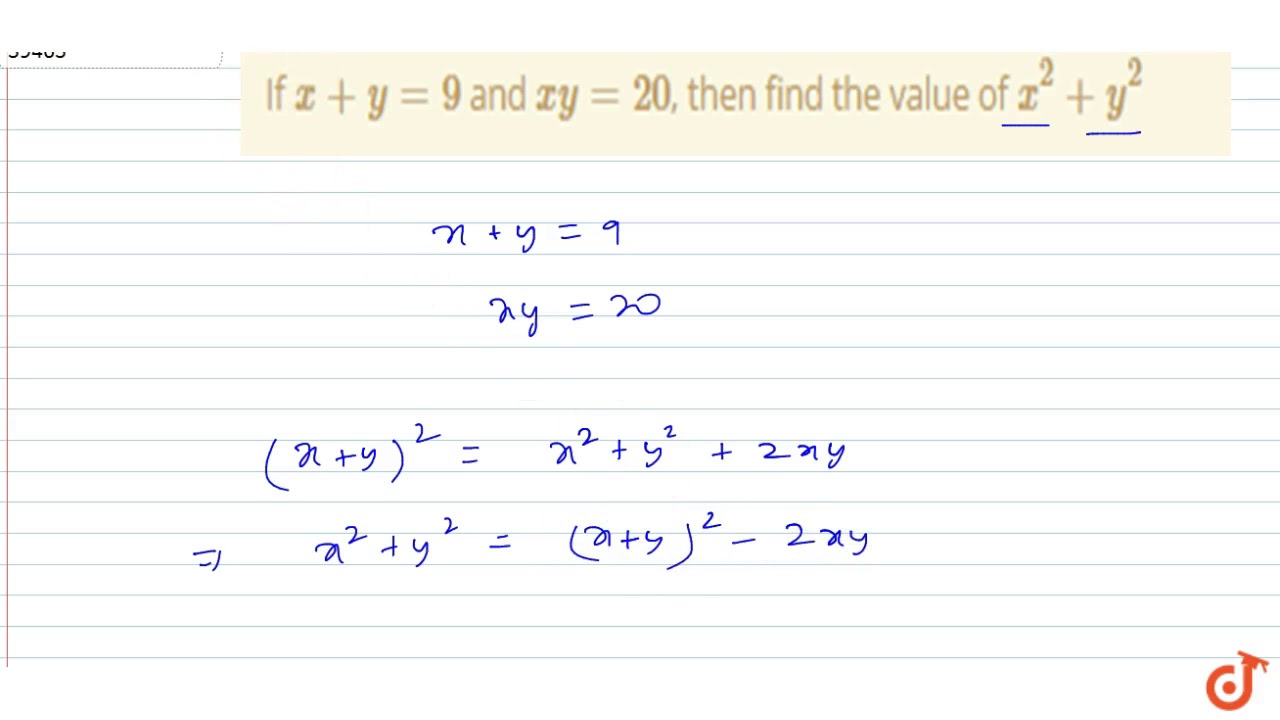



If X Y 9 And Xy Then Find The Value Of X 2 Y 2 Youtube



Class 9 Math Formula List And Tables




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In




Standard Identities Of Binomials And Trinomials Equations Examples




Snjjf Uzawyo M




If Log Xy 3 M And Log X 3 Y 2 P Find Log X 2 Y In Term Of M And P Mathematics Topperlearning Com Ge7q6onn


